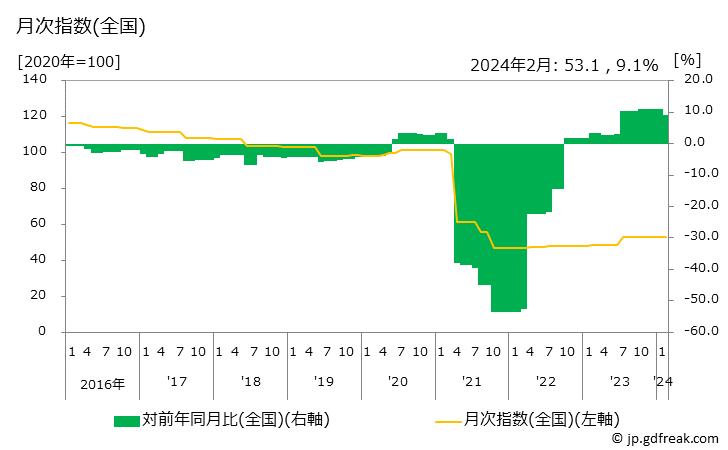
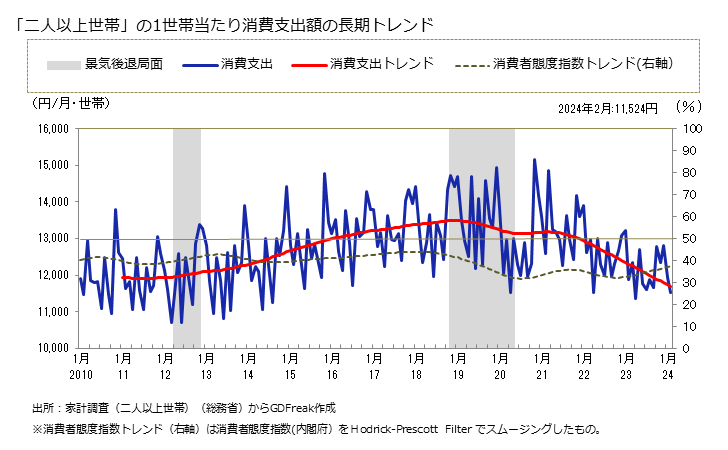
移動電話通信料の家計消費支出

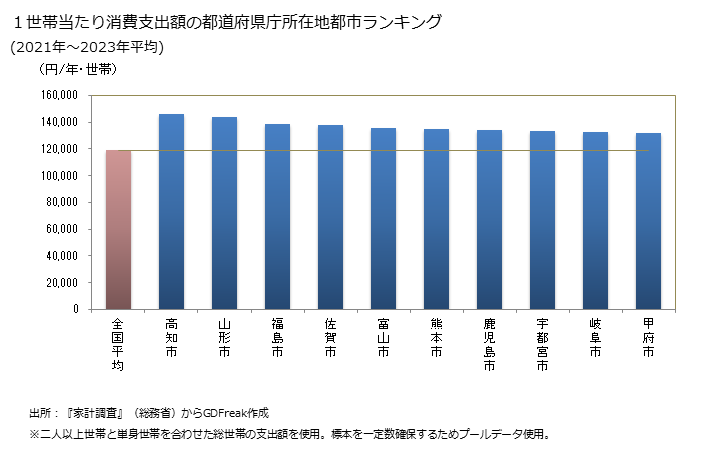
9. １世帯当たり消費支出額の都道府県の県庁所在都市によるランキング

グラフ移動電話通信料の家計消費支出１世帯当たり消費支出額の都道府県の県庁所在都市によるランキング

データ出所

総務省家計調査を基にGD Freak!が作成

ロボット君のつぶやき

このグラフは、1世帯当たり消費支出額が大きい都道府県県庁所在都市ベスト10を選び出し、大きい順にならべてみたものです。中にはやはりと思える都市あれば、おやっと驚く都市あます。人それぞれにより様々な発見ができるのではないでしょうか。
なお、統計として、ある一定の信頼性を担保するため、サンプル数を多く確保する必要があることから、ここでは2018年から2022年の５年間の平均値を用いています。それゆえに、単年ごとにみた順位と異なる場合もあるかもしれません。GD Freak では、ある程度の統計的頑健性を得るには、家計調査における標本数が必ずしも多くないことに鑑みて、どうしても5年程度の平均値で比較せざるを得ないと考えます。

(参考表) 携帯電話通信料の家計支出の都道府県ランキング(2021～2023年)

この表は、2021～2023年における都道府県の政令指定都市の携帯電話通信料の支出額の平均値とランキングの一覧表です。ランキングの上位3都市は、高知県高知市、山形県山形市、福島県福島市です。また、ランキングの下位3都市は、長崎県長崎市、京都府京都市、兵庫県神戸市です。

下の表の項目が多く見づらい場合はチェックをはずしてください。

都市名支出額(円) ランキング

[単位 : 円、順位(大きい順)]

都道府県	都市名	支出額(円)	ランキング
高知県	高知市	146,176	1
山形県	山形市	143,919	2
福島県	福島市	138,578	3
佐賀県	佐賀市	138,038	4
富山県	富山市	135,586	5
熊本県	熊本市	134,901	6
鹿児島県	鹿児島市	134,213	7
栃木県	宇都宮市	133,119	8
岐阜県	岐阜市	132,411	9
山梨県	甲府市	131,920	10
大分県	大分市	130,894	11
山口県	山口市	130,239	12
石川県	金沢市	128,543	13
茨城県	水戸市	128,482	14
島根県	松江市	128,114	15
徳島県	徳島市	127,688	16
青森県	青森市	127,606	17
秋田県	秋田市	126,682	18
新潟県	新潟市	126,348	19
北海道	札幌市	126,188	20
広島県	広島市	125,314	21
宮崎県	宮崎市	124,125	22
静岡県	静岡市	122,843	23
沖縄県	那覇市	122,703	24
宮城県	仙台市	122,245	25
岩手県	盛岡市	121,888	26
鳥取県	鳥取市	121,355	27
群馬県	前橋市	120,618	28
長野県	長野市	119,765	29
香川県	高松市	119,542	30
大阪府	大阪市	118,850	31
埼玉県	さいたま市	118,237	32
岡山県	岡山市	117,609	33
愛知県	名古屋市	116,163	34
福岡県	福岡市	116,101	35
千葉県	千葉市	115,466	36
福井県	福井市	114,381	37
滋賀県	大津市	113,396	38
三重県	津市	112,354	39
奈良県	奈良市	110,451	40
愛媛県	松山市	110,038	41
和歌山県	和歌山市	109,397	42
神奈川県	横浜市	106,490	43
東京都	23区	105,799	44
長崎県	長崎市	105,753	45
京都府	京都市	105,181	46
兵庫県	神戸市	94,730	47